Curriculum-aligned activities

e.g. 4 + (-3) - (-5)

e.g. Write the number 23 000 in standard form
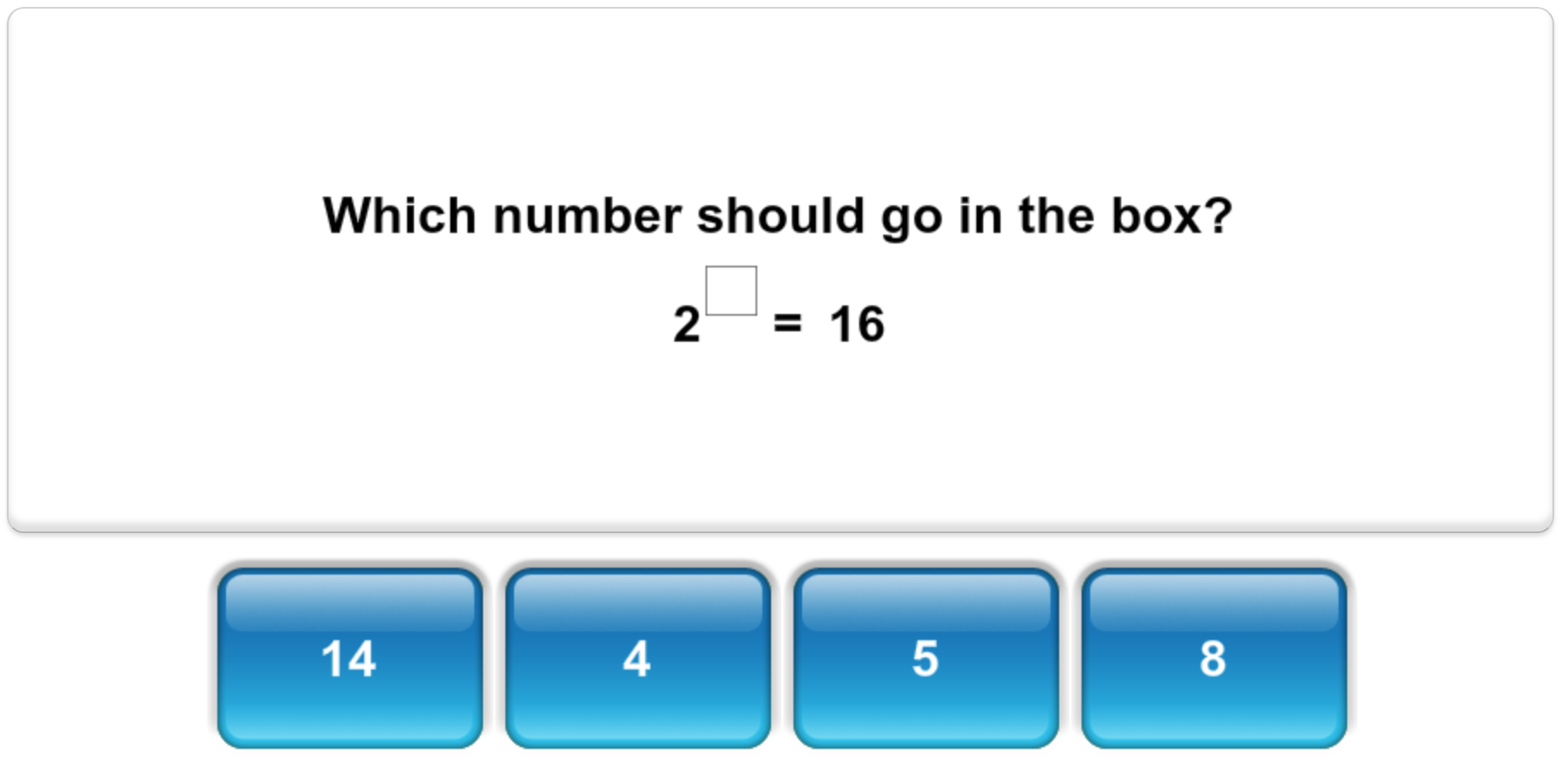
Work out answers that have powers (indices) in them. e.g. What is 7⁵ / 7³?
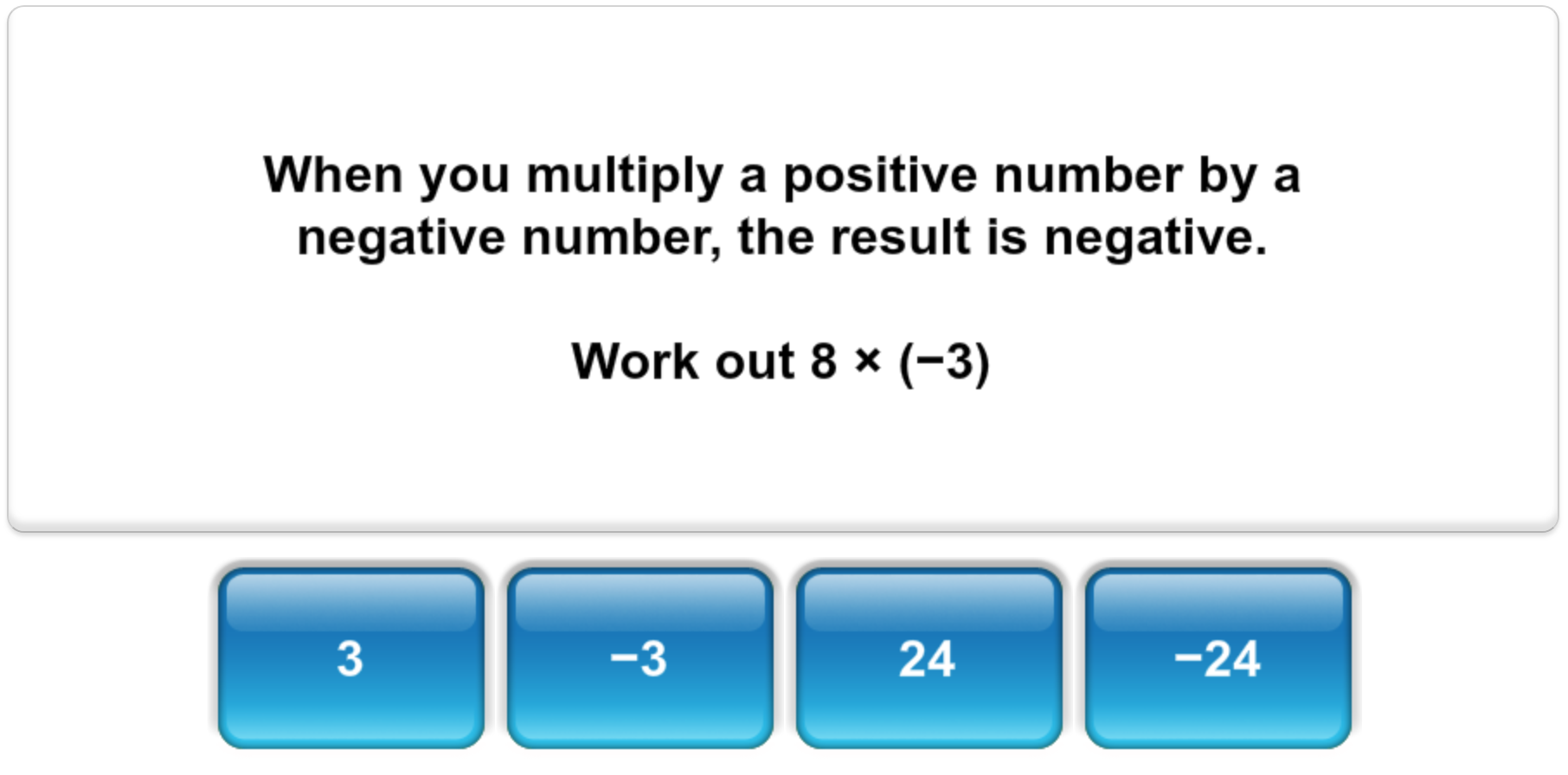
e.g. 6 x (-4)
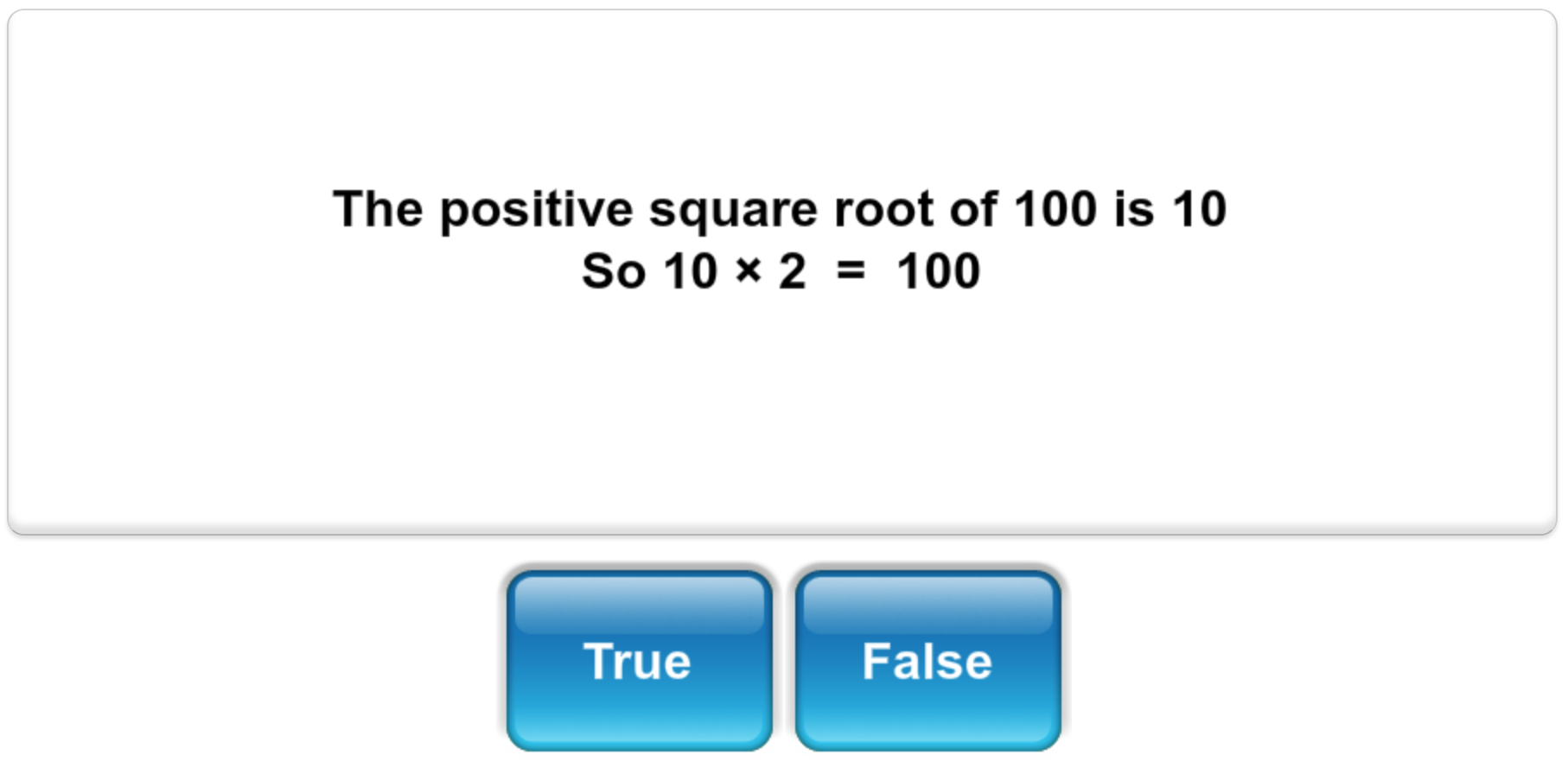
Know the square number sequence and find the square root of a number. e.g. What is the square root of 49?

Know the cube number sequence. e.g. Which of these is not a cube number? 1, 16, 125, 1000
Want a lesson plan using our activities?