De figuras simples à geometria avançada
Apply increasingly complex rules of geometry to help an imprisoned mummy swing across pits and escape its pyramid prison
Apply increasingly complex rules of geometry to help an imprisoned mummy swing across pits and escape its pyramid prison
Atividades vinculadas ao currículo
Understand that the perimeter means the total distance around a shape. Calculate the perimeter of polygons based on rectangles and triangles.
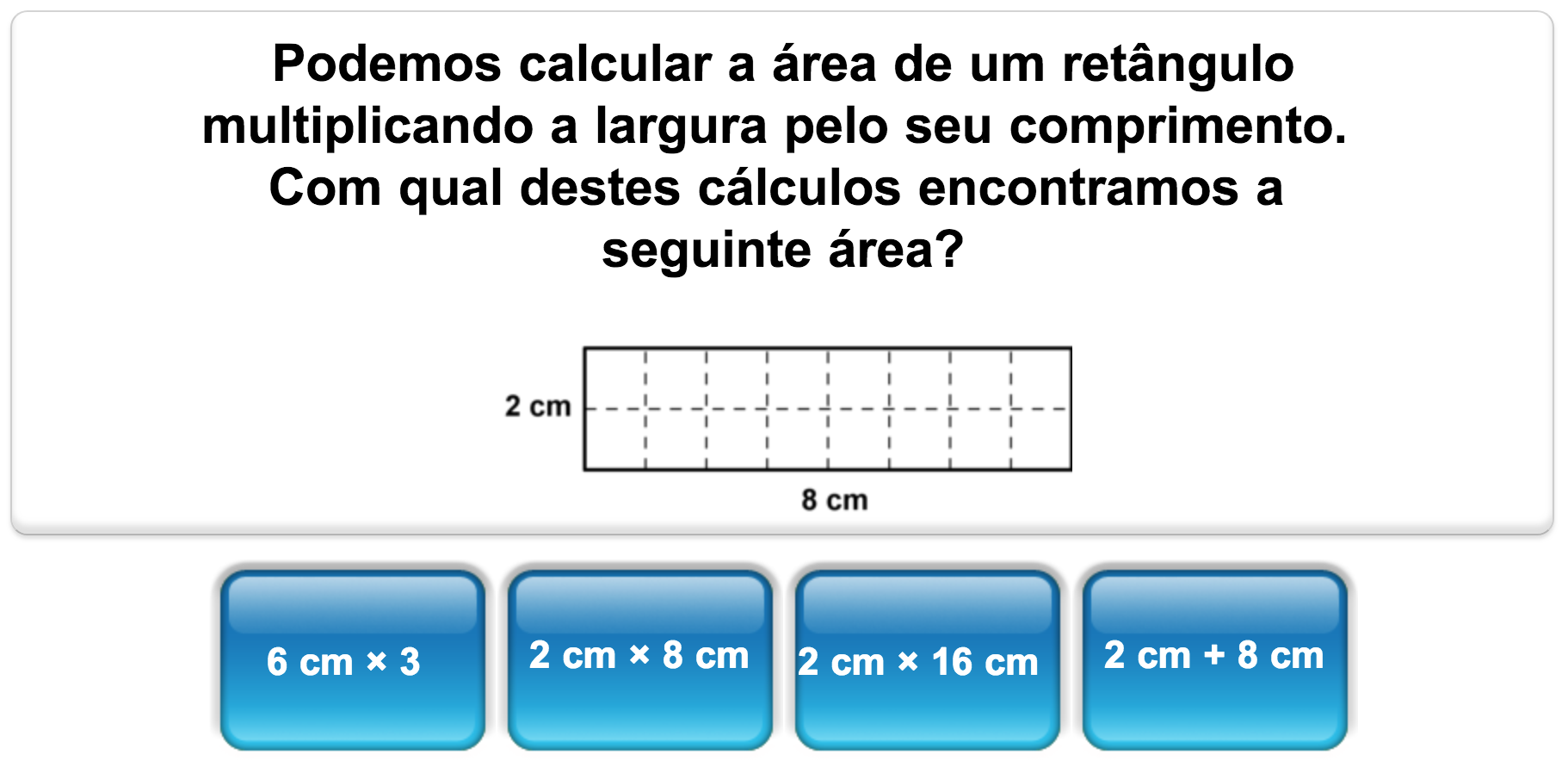
Usar a fórmula da área de um retângulo para calcular a área de um retângulo.
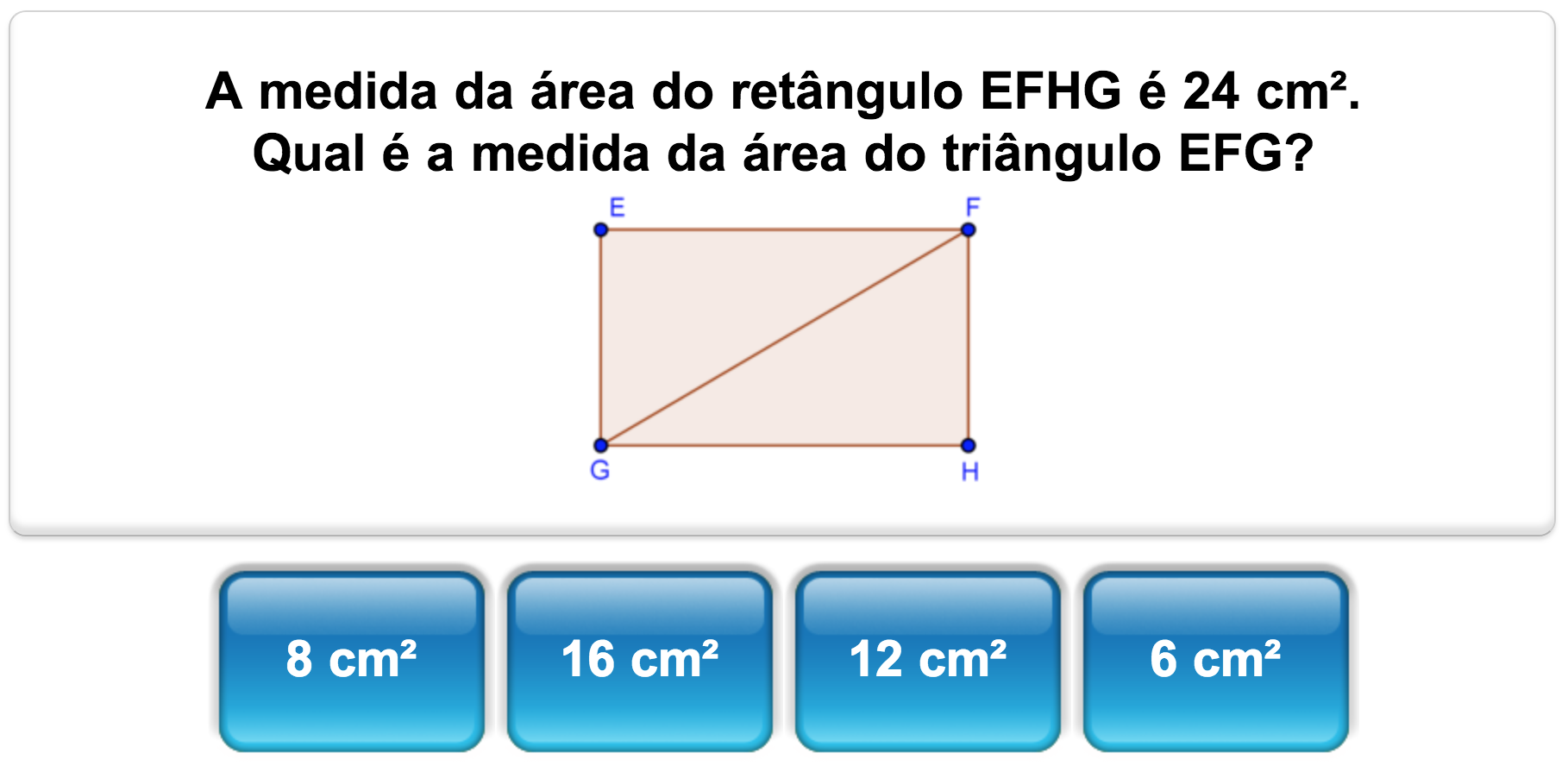
Calculate the area of a triangle using the base length multiplied by the perpendicular height, then divided by 2. Include reverse problems e.g. find the perimeter or some side given the area. Derive the formula by considering the rectangle being halved.
Know the formula for Pythagoras and use it to find the length of the longest side in a right angled triangle.
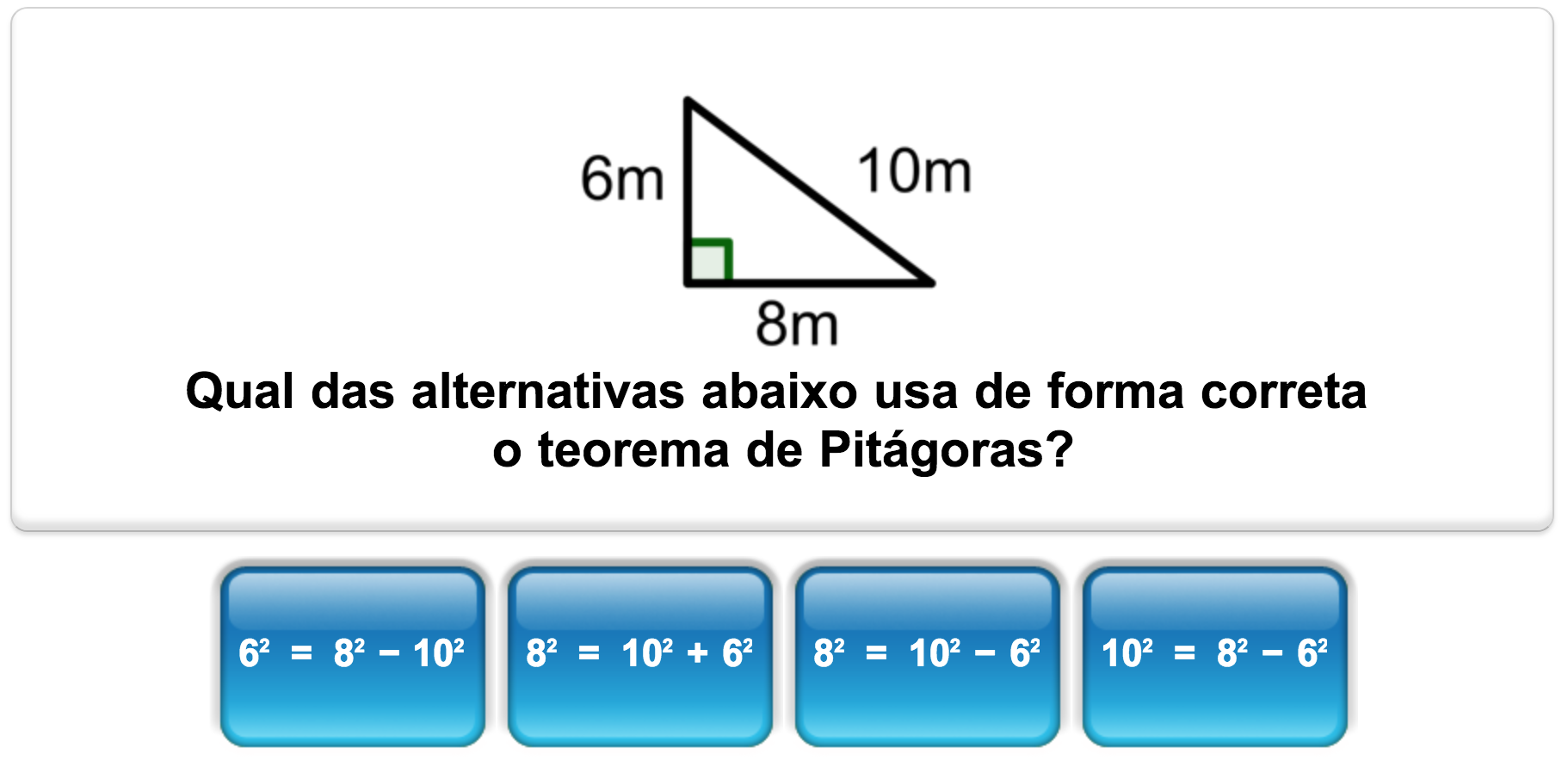
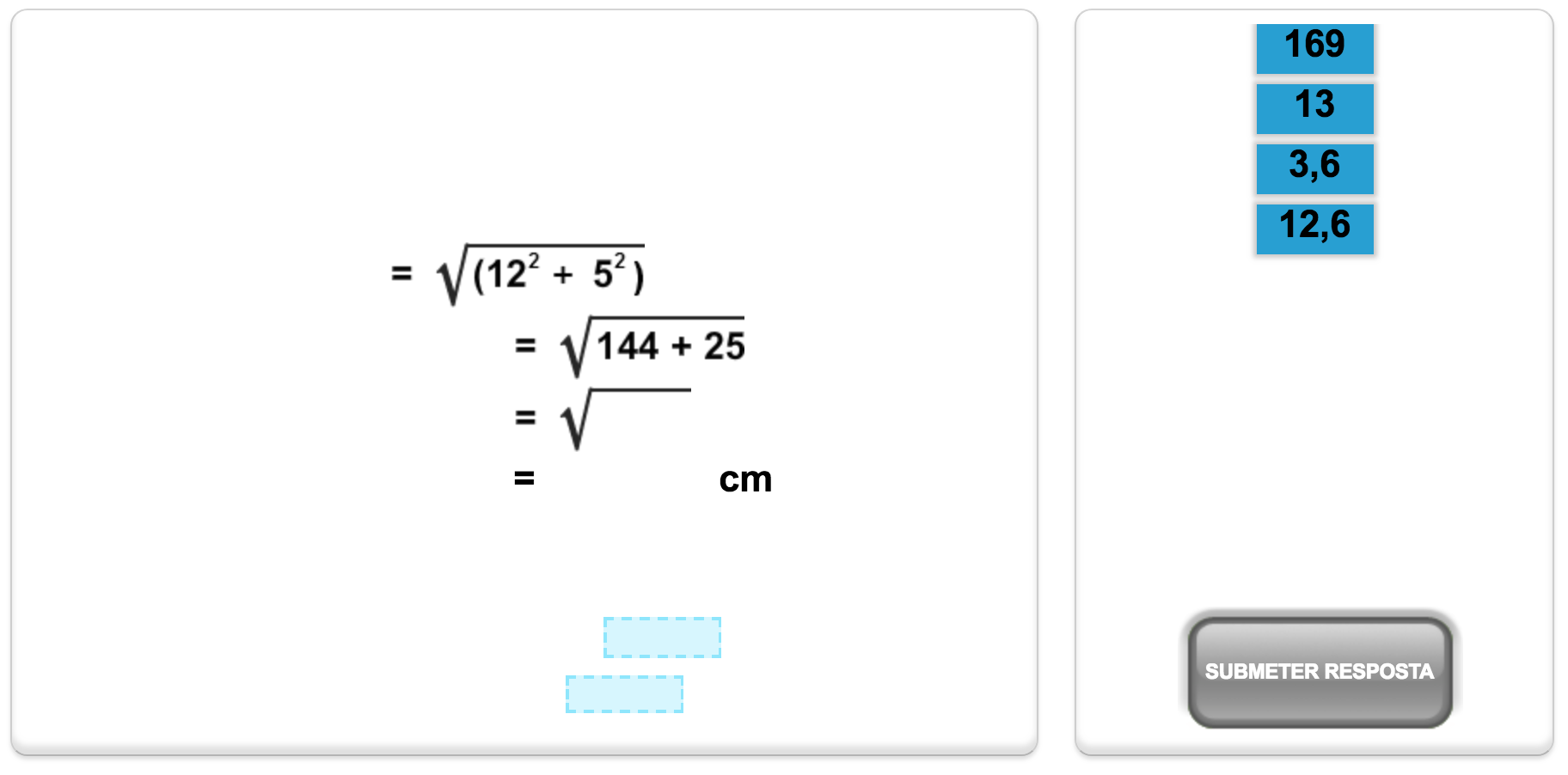
Know the formula for Pythagoras and use it to find the length of one of the shorter sides in a right angled triangle.
Utilizar o Teorema de Pitágoras para confirmar se um triângulo é retângulo.
Gostaria de ter planos de aula com as nossas atividades?
