By Prof. Marcus Du Sautoy
Time and Mathematics
I always love this time of year. In the UK for someone in the education profession it is a time of new beginnings. The start of a new academic year. A chance to learn new things. In other regions of the world there are different dates that mark the beginning of the circle of time. But of course from a mathematical point of view the point about a circle is that there is no beginning or end. It is fascinating to explore how much of the marking of the passage of time is culturally determined and how much is universal and how much is driven by mathematics.
 The year corresponds to the time it takes for the earth to orbit the sun which is the same wherever you are on earth. A day is also universal across the earth. But why did we divide the day into 24 hours? The hour into 60 minutes? Here we see human choices being made. What is fascinating is that those choices were probably driven by the mathematical properties of the numbers 24 and 60. These are highly divisible numbers which makes them perfect for dividing time into smaller units.
The year corresponds to the time it takes for the earth to orbit the sun which is the same wherever you are on earth. A day is also universal across the earth. But why did we divide the day into 24 hours? The hour into 60 minutes? Here we see human choices being made. What is fascinating is that those choices were probably driven by the mathematical properties of the numbers 24 and 60. These are highly divisible numbers which makes them perfect for dividing time into smaller units.
Human attempts to understand the passing of time are intimately connected with our first explorations into mathematics. To measure time passing requires seeing something repeating: the sun appearing each morning, your heart beating in your body, the drip of water from a pot used to create a water clock in Ancient Egypt. This ability to spot a repeating pattern is at the heart of what mathematics is all about. Mathematics is the science of pattern searching.
One of the earliest mathematical artifacts housed in the Royal Belgian Institute of Natural Sciences in Brussels is a bone covered in carved notches. Called the Ishango bone it was discovered in the Congo in 1960 but dates back 20,000 years. The notches are believed to be marking the passage of time, perhaps each notch marking a day. Keeping track of the passing days would give someone an advantage in knowing when to sew or harvest crops.
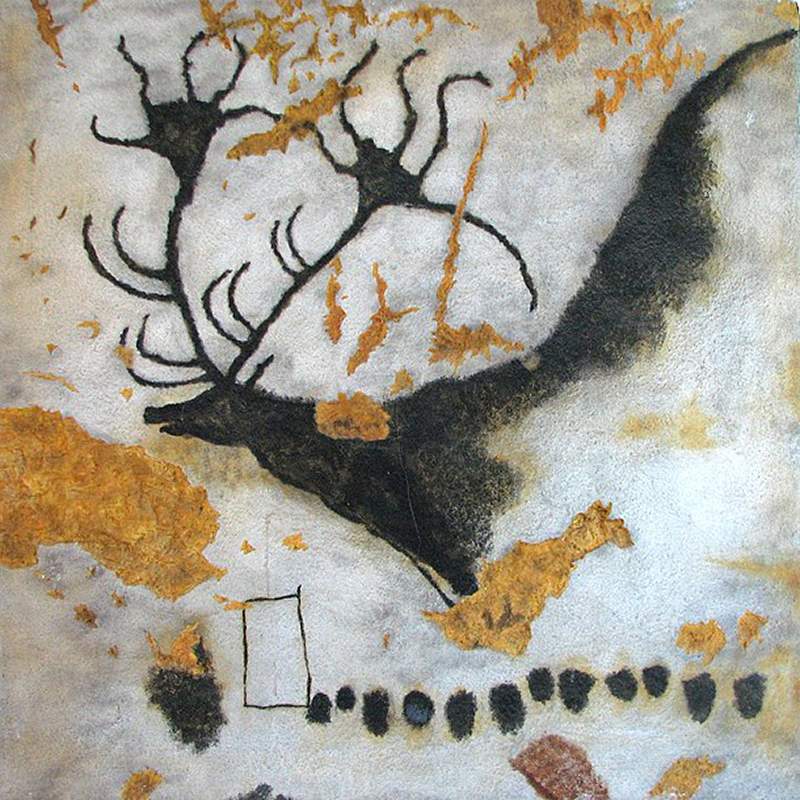 We see a different sort of calendar painted on the walls of the Lascaux caves 17,000 years ago. As well as the beautiful pictures of animals painted on the walls you find a series of dots. One collection of dots is generally believed to be a depiction of the constellation of the Pleiades. The reappearance of this important constellation in the night sky was regarded by many ancient cultures as marking the beginning of the year. As you move from the constellation across the cave you came across a sequence of thirteen dots with a rectangle drawn at the end. Above the rectangle is a huge image of a rutting stag. Further along the wall there is a sequence of what could be counted as 26 dots with a huge pregnant cow at the end.
We see a different sort of calendar painted on the walls of the Lascaux caves 17,000 years ago. As well as the beautiful pictures of animals painted on the walls you find a series of dots. One collection of dots is generally believed to be a depiction of the constellation of the Pleiades. The reappearance of this important constellation in the night sky was regarded by many ancient cultures as marking the beginning of the year. As you move from the constellation across the cave you came across a sequence of thirteen dots with a rectangle drawn at the end. Above the rectangle is a huge image of a rutting stag. Further along the wall there is a sequence of what could be counted as 26 dots with a huge pregnant cow at the end.
The dots have been interpreted by some archaeologists as marking quarters of the moons cycle, what would become the seven days of the week. These quarters were easily identifiable symbols in the sky. 13 quarters of the moon represents therefore one quarter of a year or a season. Counting on a quarter of a year from the reappearance of the Pleiades gets you to the season of rutting stags when they are more easily hunted. 26 dots on from there can be interpreted as two lots of 13 dots representing two seasons or half a year. This gets us to the point in the year in which the bison are pregnant and again vulnerable and easily hunted.
The paintings on the wall might represent a training manual for new hunters with a calendar telling them what to hunt and at what point in the year cycle. This early evidence of keeping track of time relies on spotting patterns that repeat themselves. Identifying repeating patterns and thinking mathematically has always been key to understanding the nature of time.
If you'd like to set your students a challenge in relation to Marcus' blog post here's some activities on our platform that we think you'll love!
Or if your students want to explore how bigger numbers break down into their prime factors, why don't you point them in the direction of Sigma Prime or Sigma Prime Lite.
Let us know if you enjoyed this post and if you want to read more from Professor Marcus Du Sautoy!