Curriculum-aligned activities
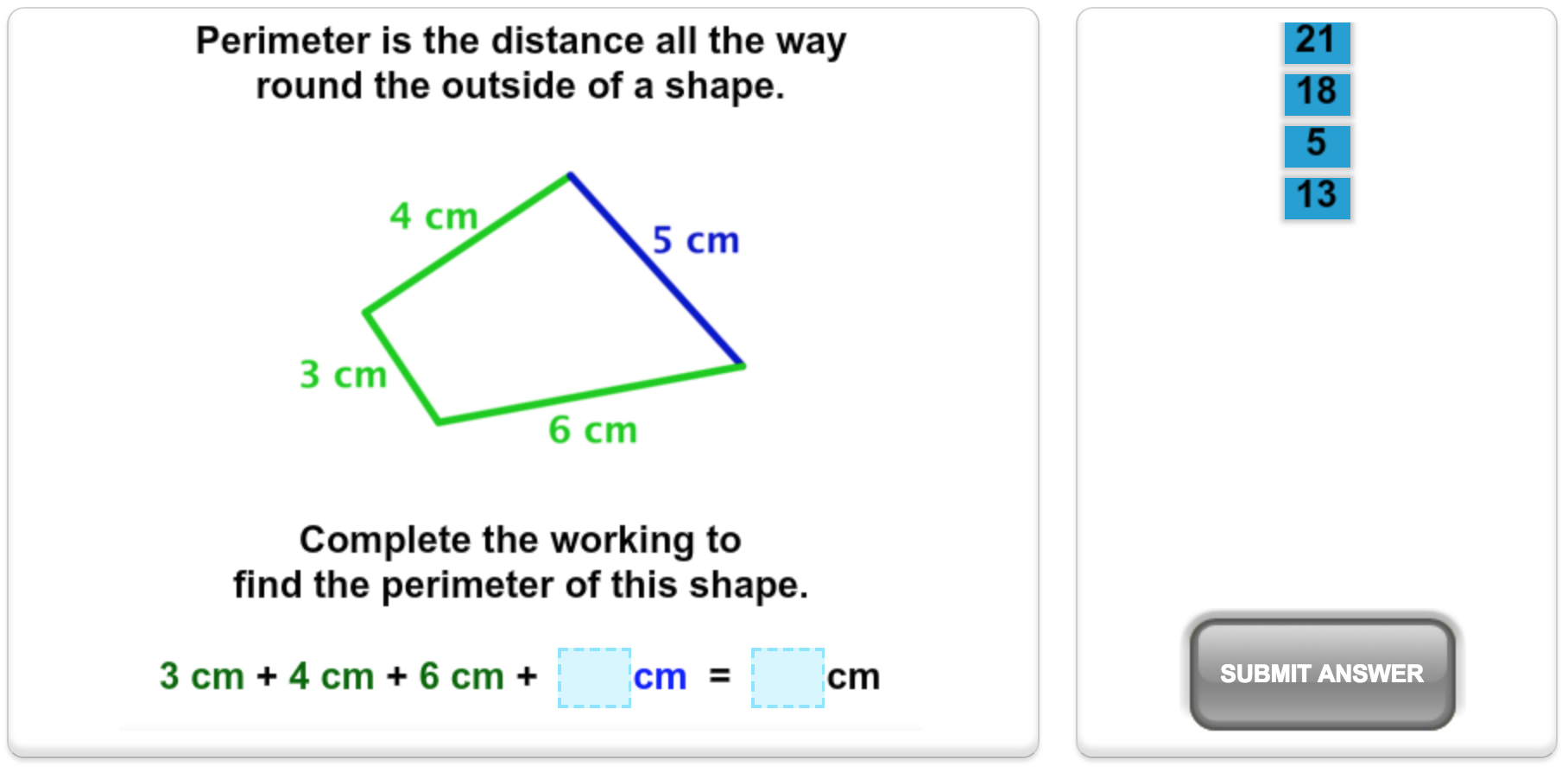
Understand that the perimeter means the total distance around a shape. Calculate the perimeter of polygons based on rectangles and triangles.
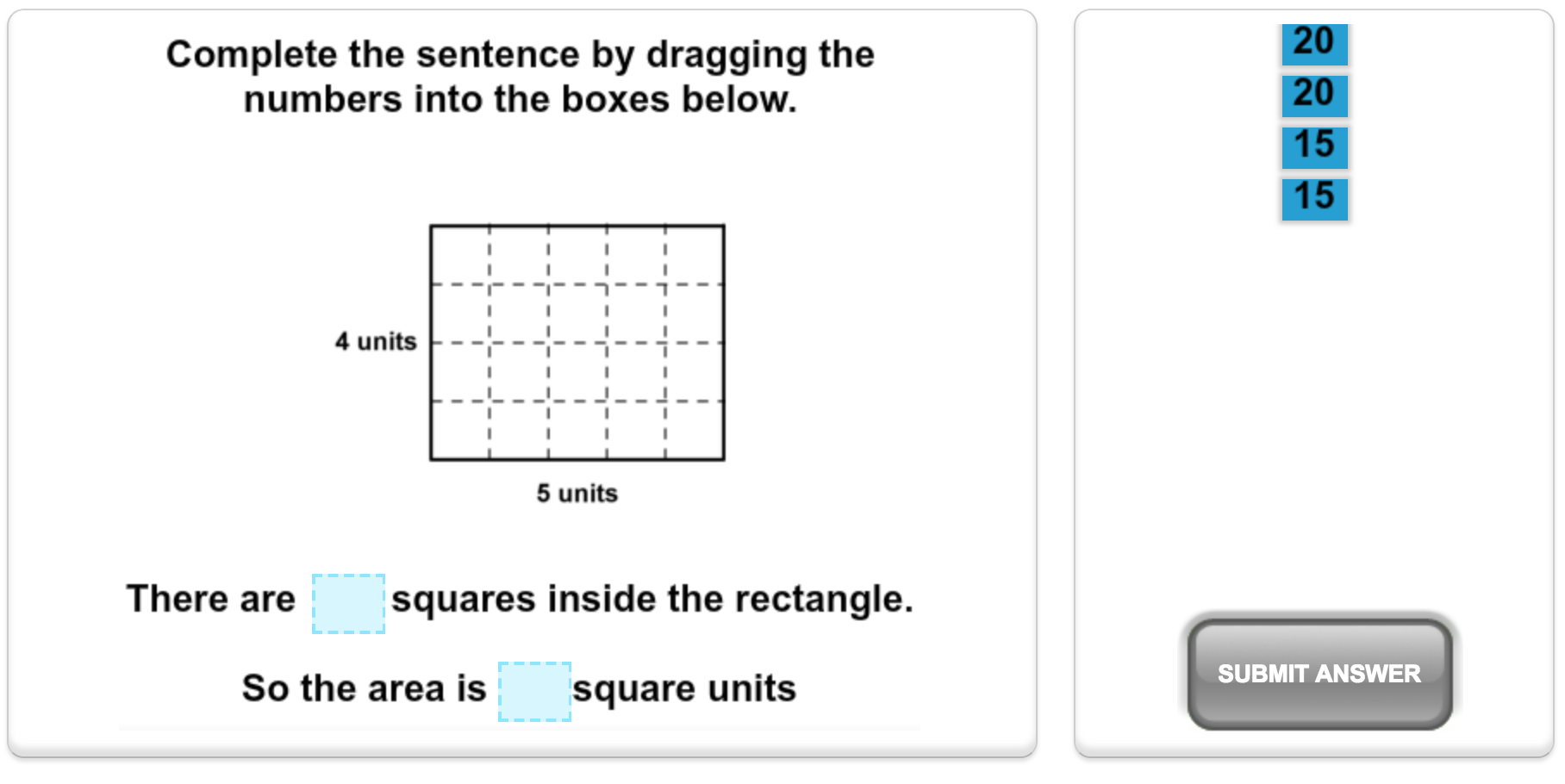
Use the formula for the area of a rectangle to calculate the rectangle's area.

Calculate the area of a triangle using the base length multiplied by the perpendicular height, then divided by 2. Include reverse problems e.g. find the perimeter or some side given the area. Derive the formula by considering the rectangle being halved.
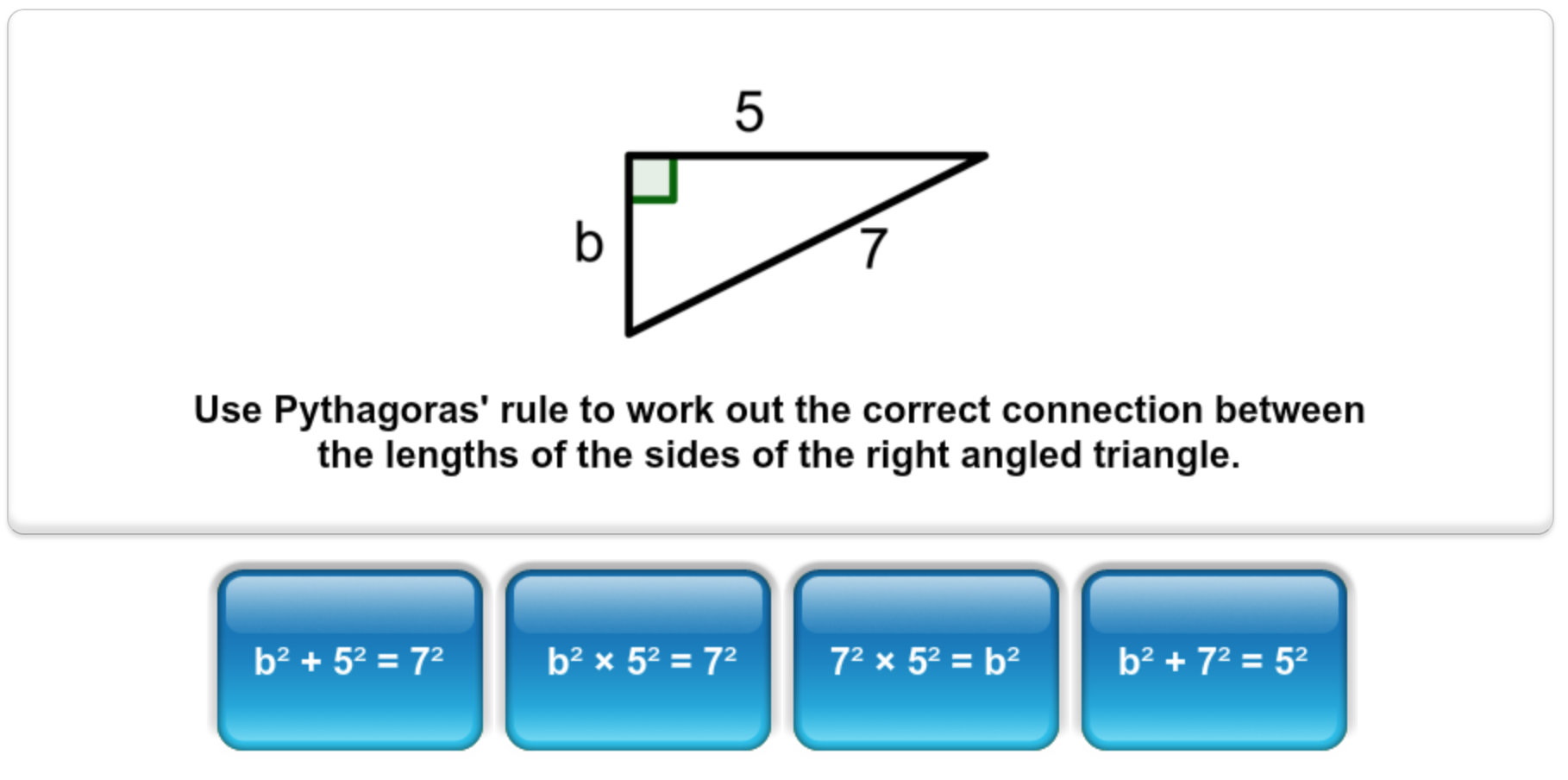
Know the formula for Pythagoras and use it to find the length of the longest side in a right angled triangle.
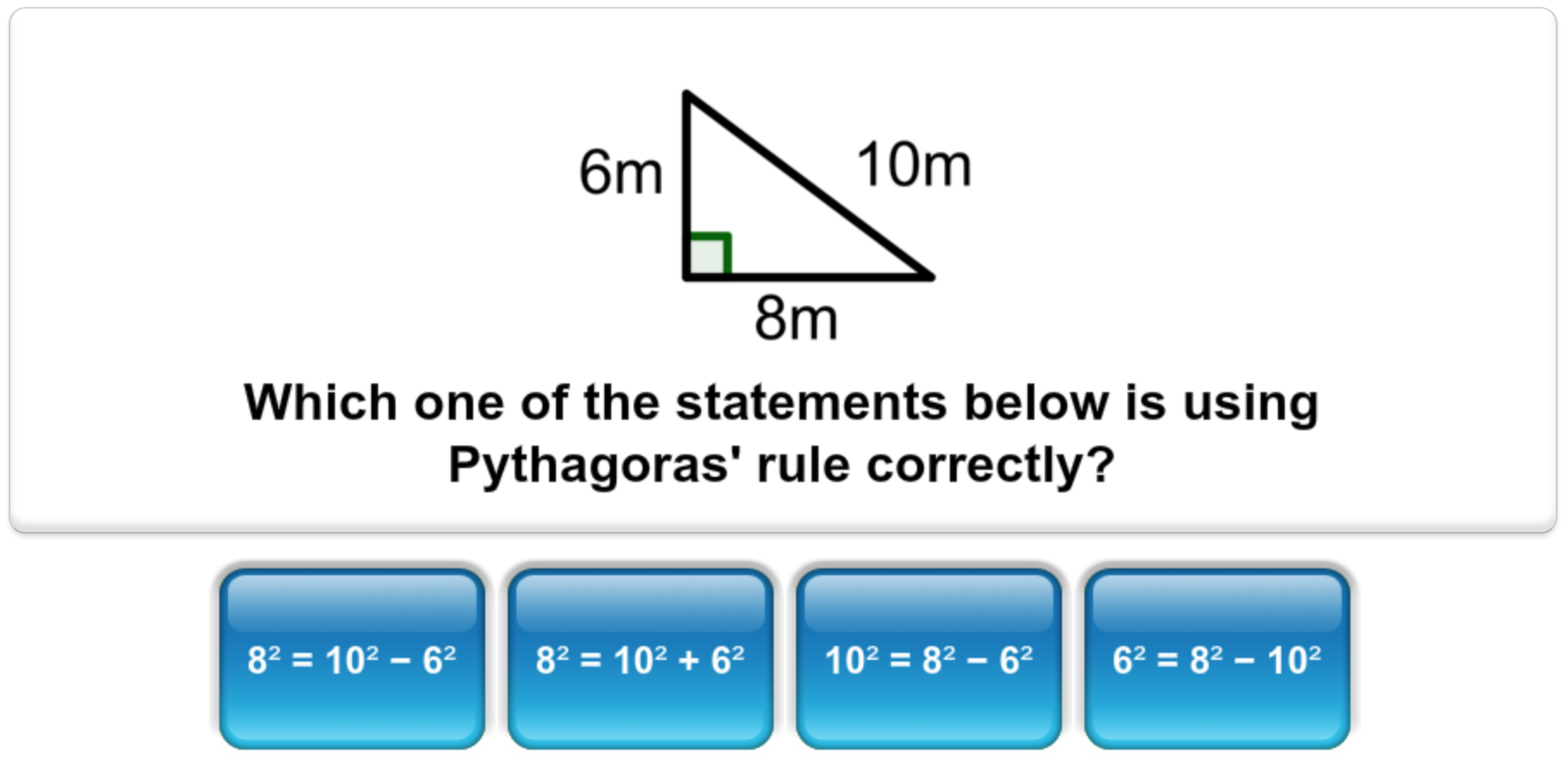
Know the formula for Pythagoras and use it to find the length of one of the shorter sides in a right angled triangle.

Use Pythagoras' theorem to find out if a triangle is right angled.
Want a lesson plan using our activities?